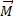
1. A metal sphere of radius R has a charge Q and is uniformly magnetized with a magnetization .Calculate the angular momentum of the field about the centre of the sphere.

The charge being uniformly distributed over its surface, the electric  field  exists only outside the sphere and  is given by 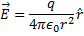. The magnetic field inside is constant and is given  outside the sphere by 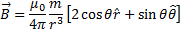.One can calculate the Poynting vector and angular momentum density closely following Problem 2 of the tutorial. The total angular momentum is obtained by integrating over all space outside the sphere.  Following this we get

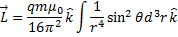
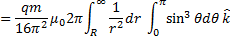
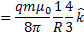
Substituting 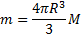, we get

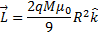
2. In Problem 1, if the magnetization of the sphere is gradually and uniformly reduced to zero (probably by heating the sphere through the Curie temperature), calculate the torque exerted by the induced electric field on the sphere and  show that the angular momentum is conserved in the process.

When the sphere is slowly demagnetized from M to zero, there is a changing flux which induces an electric field. The induced electric field is circumferential and can be calculated from Faraday’s law. The magnetic field due to the magnetized sphere inside the sphere is constant and is given by Consider a circumferential loop on the surface between polar angles  and . The radius of the circular loop is  and the area of the loop is .The changing flux through this area is and this changing flux is equal to the emf induced in the loop of radius , so that we have, the electric field magnitude to be given by

which gives,

If we consider an area element the surface, the charge on the surface experiences a force

The torque about the z axis is obtained by multiplying this with the distance of this element about the z axis.

Total torque is obtained by integrating over  the angle

The change in angular momentum is ,as was obtained in Problem 1.